Wooden sticks, when dropped on the floor, sound a variety of tones. While the bars of a xylophone are varied in tone by changing their length, these “tone bars” are all of the same length and width, but have different thicknesses and different densities and elastic properties
When a bar strikes the floor, the restoring forces of the wood cause the bar to flex back and forth.
The fundamental vibrational mode has a wavelength (λ) approximately twice the length (L) of the bar: λ ≈ 2L. The fundamental frequency is f = v / l, where v is the speed of sound in the wood. The value of v depends on the Young’s modulus (how springy the wood is) and r, the density per unit length (how much mass gets moved around) : v = sqrt(Y/r).

Tone bars by Max Kohl

The same bars from the side, showing the differences in thickness between them
More complicated analysis shows that nodes for the fundamental mode occur about one quarter of the way in from each end; in reality, 22.4% from the ends.
Fundamental: f1 ≈ 1.028 (a/L2) √(Y/ρ)
Harmonics: fn ≈ 0.441 (n + 0.5)2 f1
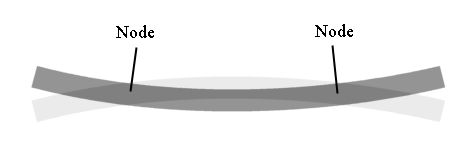
Fundamental vibrational mode
The following video demonstrates the tone bars in action; 8 bars are dropped, covering a full octave (DO-RE-MI-FA-SO-LA-TI-DO).
